Have you ever wondered how statisticians predict the outcomes of experiments involving yes-or-no answers or success and failure situations? How can they be so sure of the chances when tossing a coin, flipping a switch, or guessing on a test? The answer often lies in a powerful statistical tool known as the binomial distribution table. But what exactly is this table, and how can it help us better understand probability? Let’s dive into the world of binomial distributions in a way that’s both approachable and easy to understand.
What Is a Binomial Distribution?
Before we get into the table, let’s break down the concept of a binomial distribution. At its core, a binomial distribution deals with two possible outcomes for a given event—think heads or tails, success or failure, yes or no. These outcomes are often called binary outcomes because they have only two possible results.
For example, imagine you’re tossing a coin. There are only two potential results—heads or tails. Now, if you tossed that coin ten times, you could count how many heads (or tails) you get. This kind of situation is a classic example of a binomial distribution.
Each event—each toss, for instance—is called a trial. And when you have multiple trials, like tossing the coin ten times, you start dealing with a binomial distribution. The distribution tells you how likely it is to get a certain number of successes (in our case, heads) over a given number of trials.
Why Do We Use the Binomial Distribution Table?
So, why do we need a table for this? Why not just figure it out on the spot? Well, while it’s possible to calculate these probabilities by hand, it can be quite tricky as the number of trials increases. The binomial distribution table simplifies this process, giving us quick access to probabilities for different numbers of successes and trials.
The table allows you to easily find the probability of getting exactly k successes in n trials, given a probability of success p. Instead of having to run the numbers yourself, the table provides pre-calculated values for different scenarios, saving you time and reducing the chance of error.
Understanding the Binomial Formula
To fully appreciate the binomial distribution table, it helps to know the formula behind it. Don’t worry—we’ll break it down in simple terms. The binomial probability formula is:
P(X=k)=(nk)⋅pk⋅(1−p)n−kP(X = k) = \binom{n}{k} \cdot p^k \cdot (1 – p)^{n-k}P(X=k)=(kn)⋅pk⋅(1−p)n−k
Here’s what each part means:
- P(X = k): The probability of getting exactly k successes.
- n: The total number of trials.
- k: The number of successes you want.
- p: The probability of success on a single trial.
- (1 – p): The probability of failure on a single trial.
The formula may look intimidating, but the table takes care of most of the heavy lifting. Still, it’s helpful to understand that the table is built on this formula.
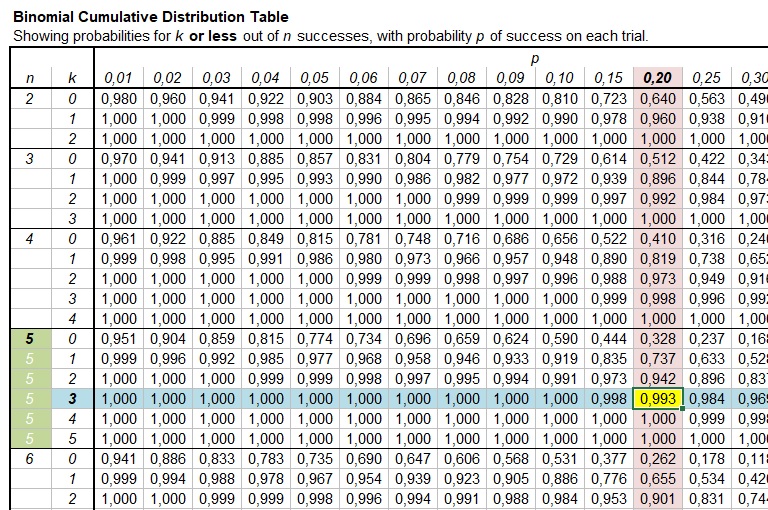
How to Read a Binomial Distribution Table
Reading a binomial distribution table is easier than it might seem. These tables are generally set up with the number of trials (n) listed down the rows and the number of successes (k) across the columns. The table entries give you the probability of getting exactly k successes out of n trials.
Let’s look at a simple example: Suppose you flip a fair coin three times. You want to know the probability of getting exactly two heads. The binomial distribution table would show you the probability for 2 successes (heads) out of 3 trials (flips), assuming a 50% chance of heads for each flip.
By referencing the table, you can quickly see the probability without needing to calculate it manually. For each new situation, the table helps you determine the likelihood of various outcomes.
Real-World Applications of Binomial Distribution
You might be thinking, “This sounds interesting, but when would I use this in real life?” The binomial distribution table has a wide variety of real-world applications, from business and economics to biology and psychology.
For example, consider quality control in a factory. Let’s say a company produces thousands of lightbulbs each day, and they know that, on average, 2% of their bulbs are defective. Using a binomial distribution table, they can easily predict the probability of finding a certain number of defective bulbs in a random sample of 100 bulbs. This helps them ensure the quality of their product while avoiding the cost and effort of testing every single item.
In medicine, researchers use binomial distributions to understand drug effectiveness. If a new medication works for 70% of patients in clinical trials, a binomial distribution table can help predict how many successful treatments they’ll see in future tests or applications.
In education, teachers might use binomial distributions to analyze test results. For example, if a teacher knows that students typically answer 60% of questions correctly, they can predict how many students will pass or fail a test based on those probabilities.
Common Misconceptions About Binomial Distribution Tables
While binomial distribution tables are incredibly useful, there are a few misconceptions that can trip people up. One common misunderstanding is that the table only works for situations with a 50/50 chance of success. The binomial distribution can handle any probability of success, whether it’s 10%, 90%, or anything in between. The key is knowing the value of p, or the probability of success in each trial, which the table will account for.
Another misconception is that binomial distributions are only used for small numbers of trials. While it’s true that the table becomes more complex with a higher number of trials, it still works for large datasets. Statisticians often use binomial distribution tables in situations with hundreds or even thousands of trials.
When to Use a Binomial Distribution Table (and When Not To)
Now that you know what a binomial distribution table is and how to use it, you might wonder when to use it. The binomial distribution is best for situations where:
- There are two possible outcomes (success or failure).
- The probability of success is the same for each trial.
- The number of trials is fixed.
However, if the probability of success changes from trial to trial, or if there are more than two possible outcomes, a different statistical method might be more appropriate. In those cases, you might look into using the Poisson distribution or normal distribution, depending on the scenario.
Conclusion: Making the Most of the Binomial Distribution Table
The binomial distribution table is a powerful and versatile tool that can help you quickly and accurately predict the likelihood of various outcomes in situations with two possible results. Whether you’re analyzing a medical study, managing quality control, or predicting test results, this table is a time-saver that simplifies the math behind probability.
The next time you find yourself faced with a situation where success or failure is the outcome, turn to the binomial distribution table. With a solid understanding of how to use it, you’ll be well-equipped to make predictions and decisions that are backed by reliable statistics.
So, what kind of situation in your life could you analyze with a binomial distribution table? You might be surprised how often it comes in handy!